Continuous time

trajectory estimation for 3D SLAM

from an actuated 2D laser scanner

Adrian Haarbach's master's thesis defense

abstract

“ This thesis aims at estimating trajectories for 3D SLAM applications. A continuous time formulation allows solving multiple problems inherent to the traditional discrete time approaches seamlessly, such as sensor fusion of actuated 2D laser scanner data with inertial measurements. Special care is taken when choosing an appropriate trajectory representation. The well-known ICP algorithm used for rigid registration is extended significantly so it can deal with continuous-time, multi-view registration of deformable scans. The resulting algorithm can be employed online in a time-windowed fashion to get an open-loop trajectory estimate and offline for global optimization to further reduce the drift. In contrast to previous work we are able to provide ground truth data for evaluation by extending an existing simulator so that it can simulate actuated 2D laser scanner data with corresponding inertial measurements. Experiments on synthetic data with different scenarios, noise levels and parameter settings show the versatility, stability and adaptability of our algorithm as well as its high overall accuracy.”

\[ \newcommand{\real}{\mathbb{R}} \newcommand{\rthree}{\real^3} \newcommand{\SOthree}{\mathrm{SO}(3)} \newcommand{\sothree}{\mathfrak{so}(3)} \newcommand{\SUtwo}{\mathrm{SU}(2)} \newcommand{\sutwo}{\mathfrak{su}(2)} \newcommand{\spherethree}{\mathbb{S}^3} \newcommand{\spheretwo}{\mathbb{S}^2} \newcommand{\norm}[1]{\left\|#1\right\|} \newcommand{\quat}{\vecb{q}} \newcommand{\vecb}[1]{\mathbf{#1}} \newcommand{\quatreal}{q_w} %scalar normal \newcommand{\quatvec}{\quat_{x:z}} %vector bold \newcommand{\point}{\vecb{p}} \newcommand{\pos}{\vecb{t}} \newcommand{\vel}{\vecb{v}} \newcommand{\acc}{\vecb{a}} \newcommand{\angVel}{{\Vecb{\omega}}} \newcommand{\Vecb}[1]{\boldsymbol{#1}} \newcommand{\real}{\mathbb{R}} \newcommand{\rthree}{\real^3} \newcommand{\rthreebythree}{\real^{3 \times 3}} \newcommand{\rtwo}{\real^2} \newcommand{\cloud}[1]{\mathcal{#1}} \newcommand{\cloudsize}[1]{N_{\cloud{#1}}} \newcommand{\cloudi}[1]{\left\{\MakeLowercase{#1}_i\right\}} \newcommand{\cloudr}[1]{\{\MakeLowercase{#1}_1,\MakeLowercase{#1}_2,...,\MakeLowercase{#1}_{\cloudsize{#1}}\}} \newcommand{\clouddef}[1]{\cloud{#1}=\cloudi{#1}=\cloudr{#1}} \newcommand{\cloudfull}[1]{\clouddef{#1}, \MakeLowercase{#1}_i \in \rthree} \newcommand{\scalarfull}[1]{\clouddef{#1}, \MakeLowercase{#1}_i \in \real} \def\firstToLow#1{\expandafter\firstToLowA#1!!} \def\firstToLowA#1#2!!{\MakeLowercase{#1}#2} %chapter 2 %vector bold in math mode \newcommand{\vecb}[1]{\mathbf{#1}} %http://tex.stackexchange.com/questions/3535/bold-math-automatic-choice-between-mathbf-and-boldsymbol-for-latin-and-greek %\newcommand{\vect}[1]{\boldsymbol{\mathbf{#1}}} \newcommand{\Vecb}[1]{\boldsymbol{#1}} %matrix not italic in math mode %\newcommand{\matr}[1]{\mathrm{#1}} \newcommand{\mean}{{\Vecb{\mu}}} %\bar{p} \newcommand{\Cov}{\Sigma} %normal with error \newcommand{\normal}{\vec{\vecb{n}}} \newcommand{\eigsmall}{\lambda_0} \newcommand{\eigmiddle}{\lambda_1} \newcommand{\eiglarge}{\lambda_2} \newcommand{\eigVals}{\eigsmall \leq \eigmiddle \leq \eiglarge} \newcommand{\eigsum}{\eigsmall + \eigmiddle + \eiglarge} \newcommand{\eigVecSmall}[1][]{\vecb{e}_{0#1}} \newcommand{\eigVecMiddle}[1][]{\vecb{e}_{1#1}} \newcommand{\eigVecLarge}[1][]{\vecb{e}_{2#1}} \newcommand{\eigVecs}{\eigVecSmall,\eigVecMiddle,\eigVecLarge} %NLS \newcommand{\res}{\vecb{r}} %e \newcommand{\eres}{\vecb{e}} %e for our residuals \newcommand{\factor}{}%\frac{1}{2}} %%motion \newcommand{\SOthree}{\mathrm{SO}(3)} \newcommand{\sothree}{\mathfrak{so}(3)} \newcommand{\SUtwo}{\mathrm{SU}(2)} \newcommand{\sutwo}{\mathfrak{su}(2)} \newcommand{\spherethree}{\mathbb{S}^3} \newcommand{\spheretwo}{\mathbb{S}^2} %https://en.wikipedia.org/wiki/Rotation_group_SO(3)#Quaternions_of_unit_norm %SU(2) is isomorphic to the quaternions of unit norm via a map given by %https://en.wikipedia.org/wiki/Special_unitary_group %Therefore, as a manifold S3 is diffeomorphic to SU(2) and so SU(2) is a compact, connected Lie group. \newcommand{\SEthree}{\mathrm{SE}(3)} \newcommand{\sethree}{\mathfrak{se}(3)} %interpolation \def\Bezier{B\'ezier} \def\Bspline{B-spline} %chapter 3 \newcommand{\der}{\dot} \newcommand{\dder}{\ddot} \newcommand{\derFull}[1]{\frac{d #1}{d\timeVar}} \newcommand{\dderFull}[1]{\frac{d^2 #1}{d\timeVar^2}} \newcommand{\Der}[1]{#1'} \newcommand{\Dder}[1]{#1''} \newcommand{\timeVar}{\tau} \newcommand{\curr}{(\timeVar)} \newcommand{\diff}{\Delta \timeVar} \newcommand{\tnext}{(\timeVar+\diff)} \newcommand{\midpoint}{(\timeVar+ \frac{1}{2}\diff)} \newcommand{\world}{{_w}} \newcommand{\base}{{_s}} \newcommand{\point}{\vecb{p}} \newcommand{\pos}{\vecb{t}} \newcommand{\vel}{\vecb{v}} \newcommand{\acc}{\vecb{a}} \newcommand{\angVel}{{\Vecb{\omega}}} \newcommand{\quat}{\vecb{q}} \newcommand{\ori}{\quat} \newcommand{\matrixn}[1]{\mathrm{#1}} \newcommand{\R}{\matrixn{R}} \newcommand{\I}{\matrixn{I}} \newcommand{\T}{\matrixn{T}} %SE(3) homogeneous matrix \newcommand{\rr}{\vecb{r}} %linear rotation bosse slot \newcommand{\bias}{\base\vecb{b}}%\mathrm{bias}} \newcommand{\gravity}{\world\vecb{g}}%\mathrm{gravity}}%\vecb{g}} %continuity \newcommand{\C}[1]{C\textsuperscript{#1}} %icp correspondenced \newcommand{\pp}{\point} \newcommand{\pq}{\point'} \newcommand{\np}{\normal} \newcommand{\nq}{\normal'} \newcommand{\Covp}{\Cov} \newcommand{\Covq}{\Cov'} \newcommand{\mup}{\mean} \newcommand{\muq}{\mean'} %sweeps \newcommand{\pa}{\vecb{a}} \newcommand{\pb}{\vecb{b}} %chapter 4 approach \newcommand{\NC}{ \frac{1}{6} \begin{bmatrix*}[r] 0 & 1 & -2 & 1 \\ 0 & -3 & 3 & 0 \\ 0 & 3 & 3 & 0 \\ 6 & 5 & 1 & 0 \end{bmatrix*} } \newcommand{\N}[1]{\widetilde{\mathbf{N}}_{#1}} \newcommand{\Ndot}[1]{\der{\widetilde{\mathbf{N}}}_{#1}} \newcommand{\Ndotdot}[1]{\dder{\widetilde{\mathbf{N}}}_{#1}} \newcommand{\laserScans}{\mathcal{L}} \newcommand{\imuMeas}{\mathcal{M}} \newcommand{\sweeps}{\mathcal{S}} \newcommand{\sweepDur}{\Delta\timeVar_{Sweep}} \newcommand{\taus}{\Delta\timeVar_{basePoses}} \newcommand{\timeNow}{\timeVar_{curr}} \newcommand{\matchesSurfel}{\text{surfelMatches}} \newcommand{\matchesIMU}{\text{imuMatches}} \newcommand{\expi}[1]{\exp(\N{#1}\angVel_{#1})} \newcommand{\deri}[1]{(\Ndot{#1}\angVel_{#1})} \newcommand{\veli}[1]{\N{#1}\vel_{#1}} \newcommand{\velidot}[1]{\Ndot{#1}\vel_{#1}} \newcommand{\velidotdot}[1]{\Ndotdot{#1}\vel_{#1}} % norm \newcommand{\norm}[1]{\left\|#1\right\|} %\newcommand{\normtwo}[1]{\left\|\left\|#1\right\|\right\|^2} %\newcommand{\abs}[1]{ \left\lvert#1\right\rvert} % absolute value: single vertical bars \newcommand{\Norm}[1]{\left\lVert#1\right\rVert} % norm: double vertical bars \newcommand{\determinant}[1]{|#1|} % un demi \newcommand{\half}{\frac{1}{2}} % parantheses \newcommand{\parenth}[1]{ \left( #1 \right) } \newcommand{\bracket}[1]{ \left[ #1 \right] } \newcommand{\accolade}[1]{ \left\{ #1 \right\} } %\newcommand{\angle}[1]{ \left\langle #1 \right\rangle } % partial derivative: %#1 function, #2 which variable % simple / single line version \newcommand{\pardevS}[2]{ \delta_{#1} f(#2) } % fraction version \newcommand{\pardevF}[2]{ \frac{\partial #1}{\partial #2} } % render vectors: 3 and 4 dimensional \newcommand{\veciii}[3]{\left[ \begin{array}[h]{c} #1 \\ #2 \\ #3 \end{array} \right]} \newcommand{\veciv}[4]{\left[ \begin{array}[h]{c} #1 \\ #2 \\ #3 \\ #4 \end{array} \right]} \newcommand{\bfrac}[2]{\genfrac{}{}{0pt}{}{#1}{#2}} \newcommand{\rightleftlie}{\bfrac{\xrightarrow[]{\log}}{\xleftarrow[\exp]{}}} %chapter 4 approach \]

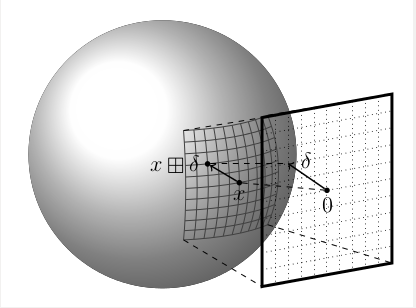
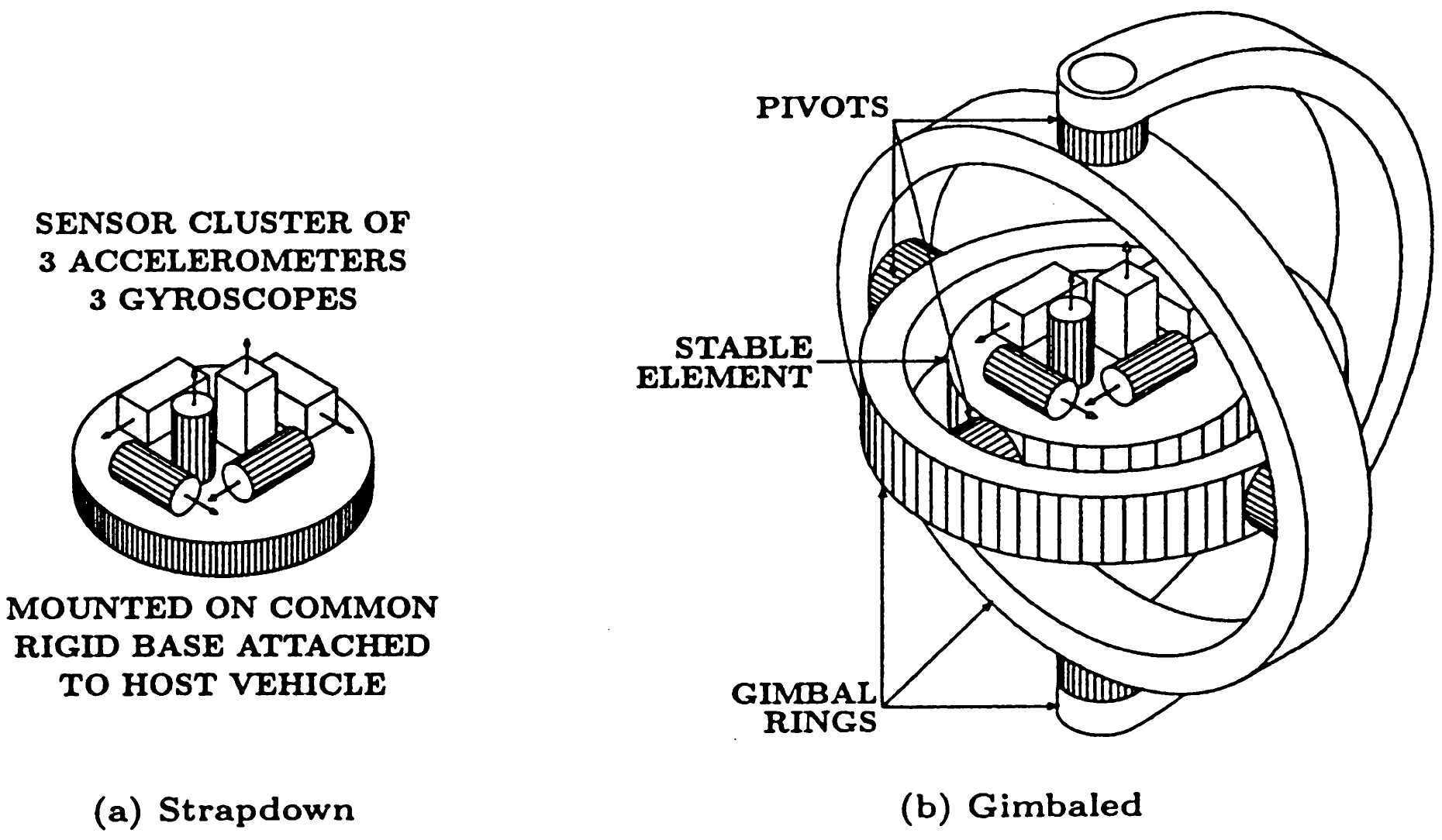
Introduction

stationary 3D scanner

actuated 2D scanner

Simultaneous Localization And Mapping (SLAM)

Background

Rigid Body motion

\[ \begin{align} \text{Lie group} & \rightleftlie \text{Lie algebra} \\ \\ \mathrm{SO}(3) &\rightleftarrows \mathfrak{so}(3) \\ \mathrm{SU}(2) &\rightleftarrows \mathfrak{su}(2) \\ \mathrm{SE}(3) &\rightleftarrows \mathfrak{se}(3) \end{align} \]

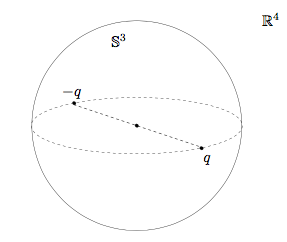
unit quaternions \(\boxed{\SUtwo \cong \spherethree \cong \mathbb{H}_1 = \{\quat \in \mathbb{H} | \norm{\quat} = 1 \}}\)

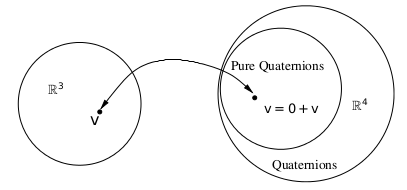
pure quaternions \(\boxed{\sutwo \cong \rthree \cong \mathbb{H}_0 = \{\quat \in \mathbb{H} | \quatreal = 0 \}} \)

\( \quat \in \spherethree \cong \SUtwo \rightleftlie \angVel \in \rthree \cong \sutwo \)

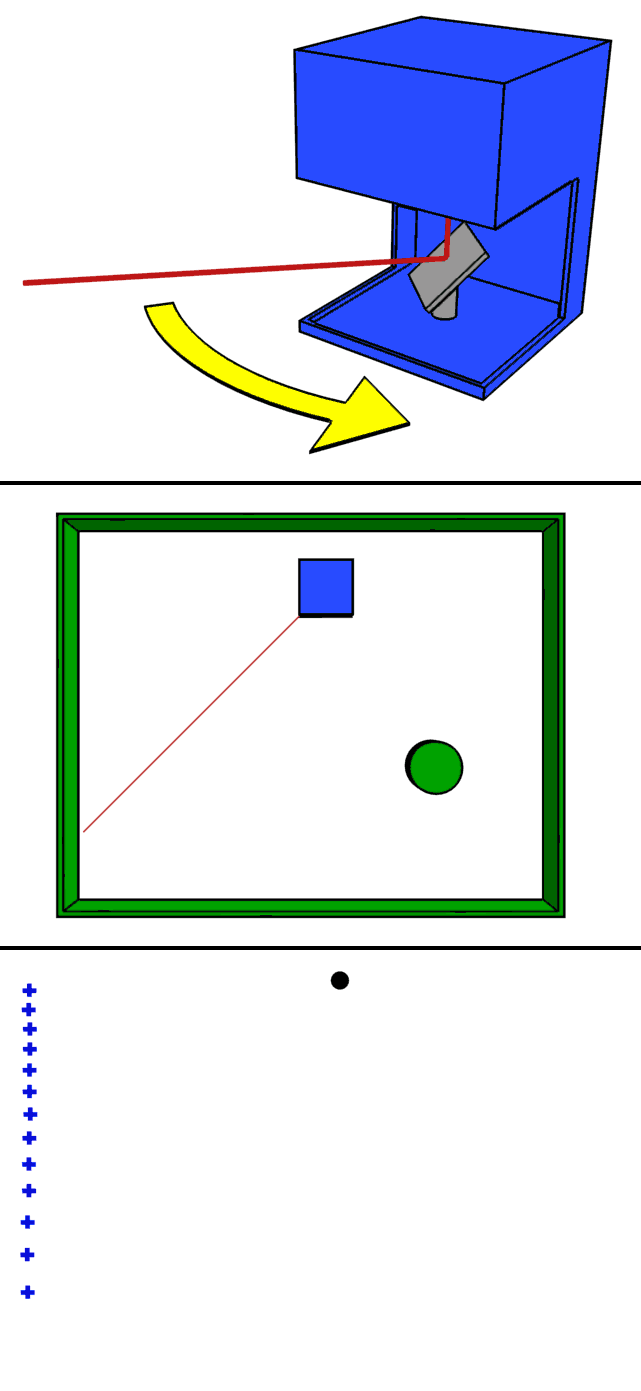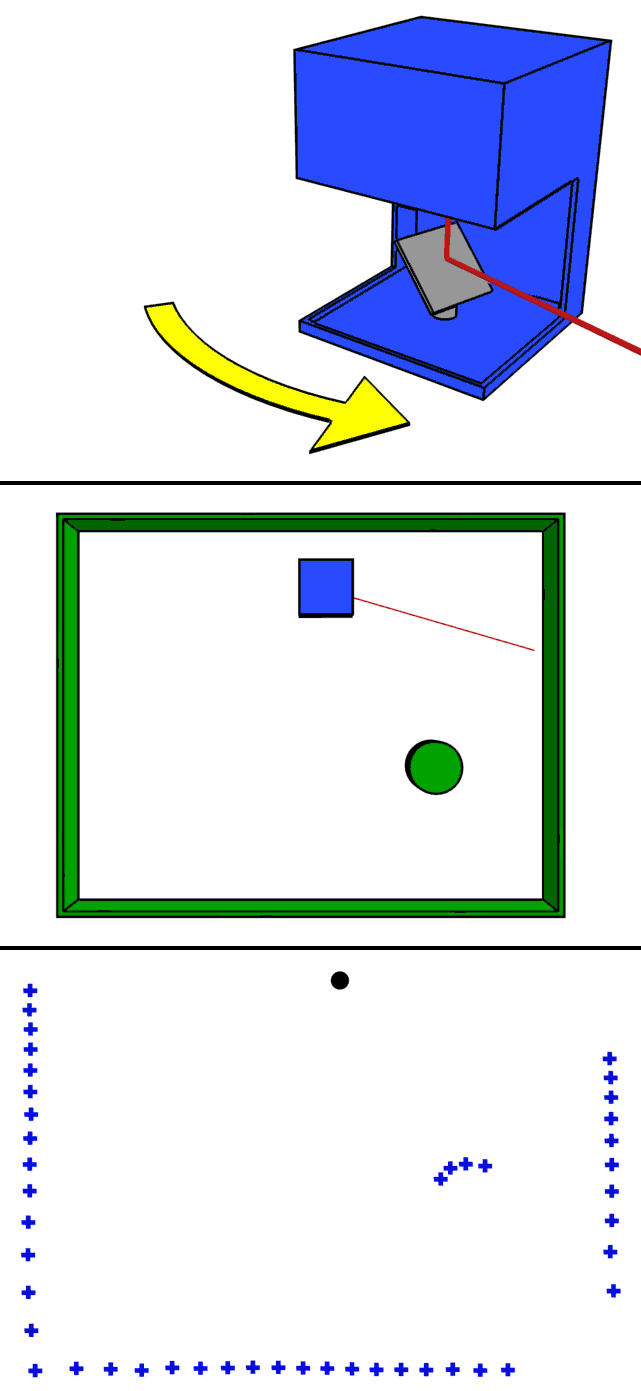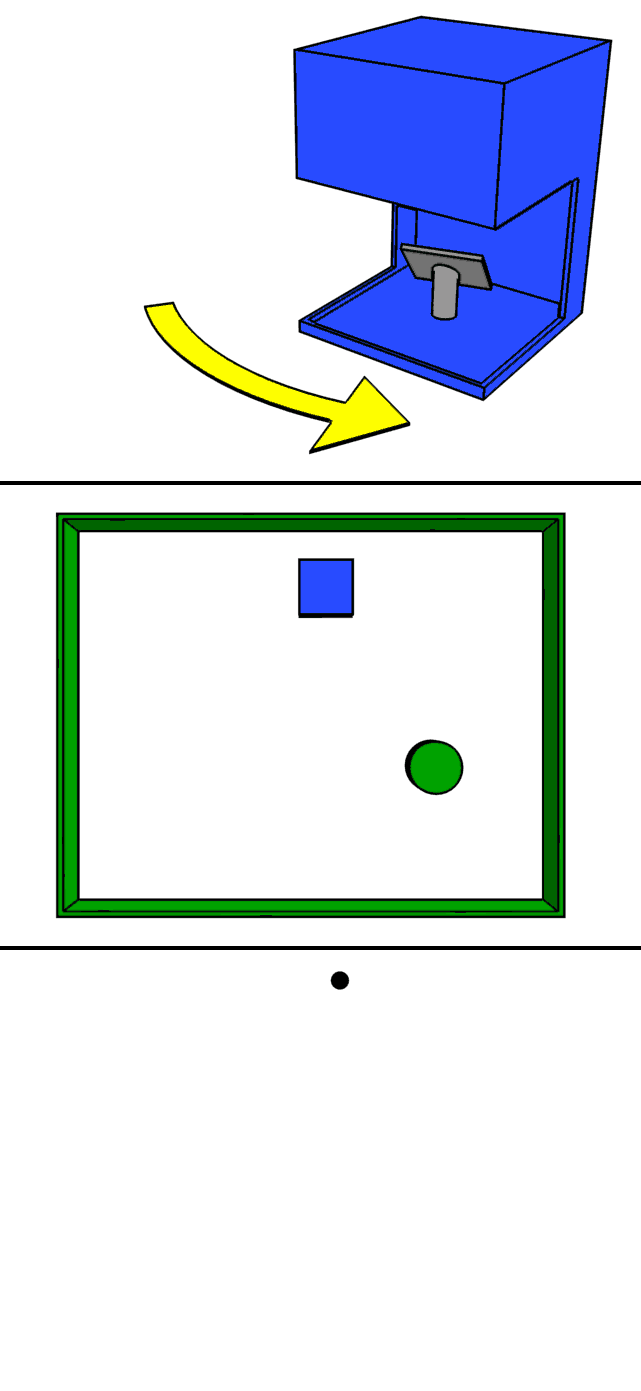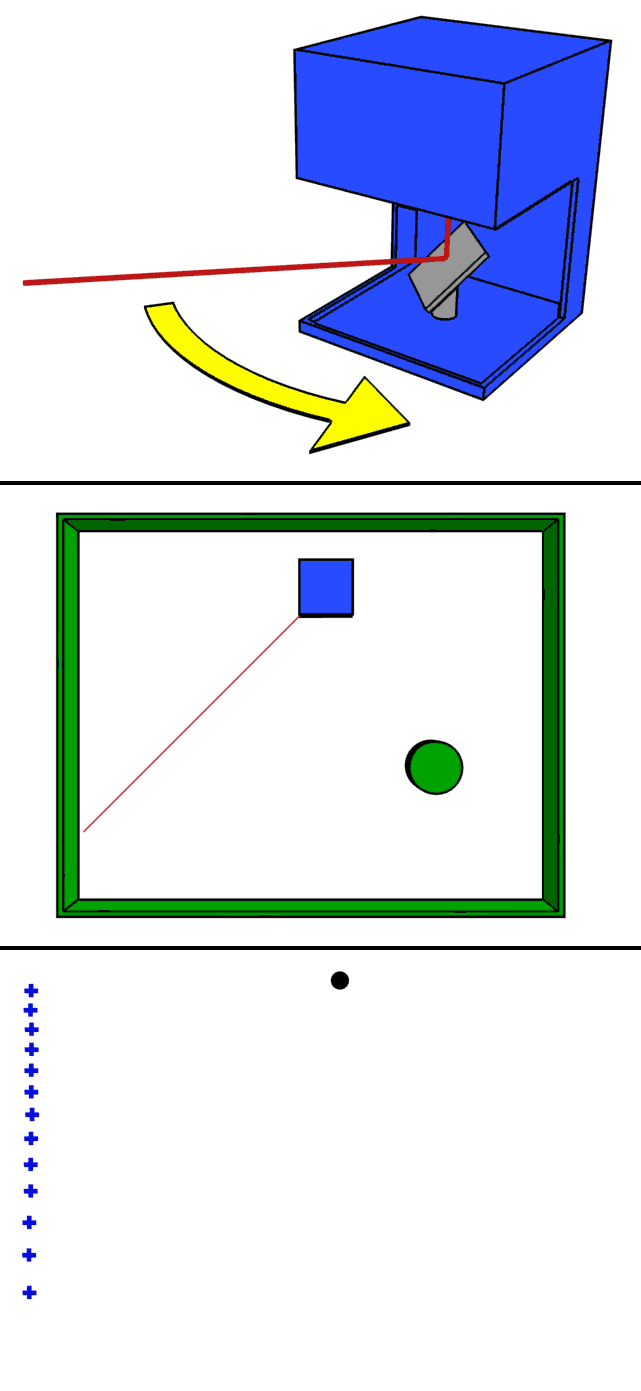
Sensors - LiDAR

Light Detection And Ranging

4,5kg	1,1kg	0,3kg	weight
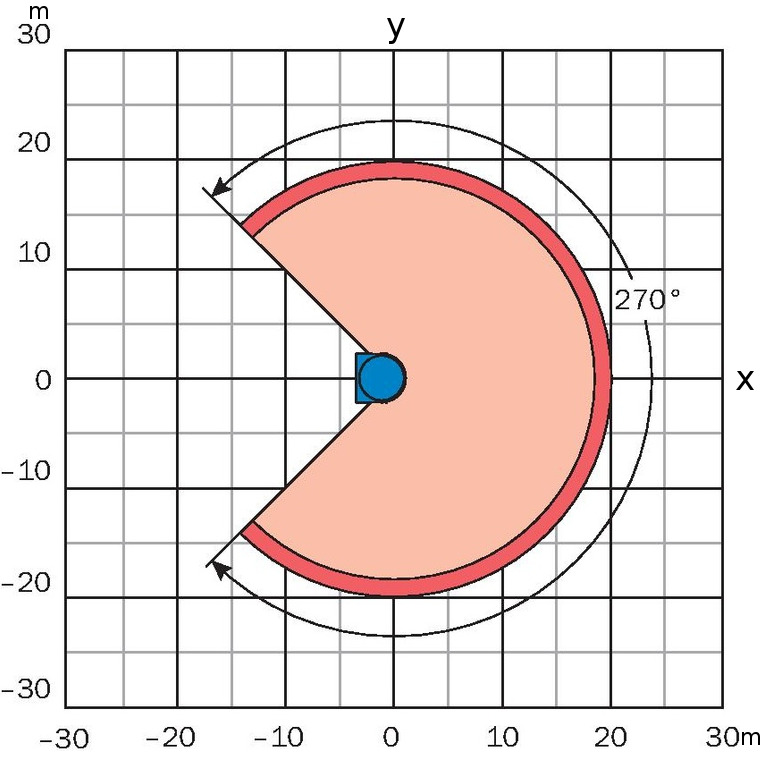
180°	270°	270°	fov
1,00°	0,50°	0,25°	res.
13.500	27.000	43.200	pts/s

\( \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} r\cos(\phi)\\ r\sin(\phi) \end{pmatrix} \\ \phi = \phi_0 + i\Delta\phi \)

Sensors - IMU

Inertial Measurement Unit


\( \newcommand{\angVelMeas}{\base\tilde\angVel\curr & = \base\angVel\curr + \bias_\angVel\curr + \mathcal{N}(\vecb{0},\vecb{\sigma}_\angVel)} \newcommand{\accMeas}{\base\tilde\acc\curr & = \base\acc\curr + \bar{\ori}\curr \gravity + \bias_\acc\curr + \mathcal{N}(\vecb{0},\vecb{\sigma}_\acc)} \begin{align} \angVelMeas &\text{angVel}\\ \accMeas &\text{linAcc} \end{align} \)

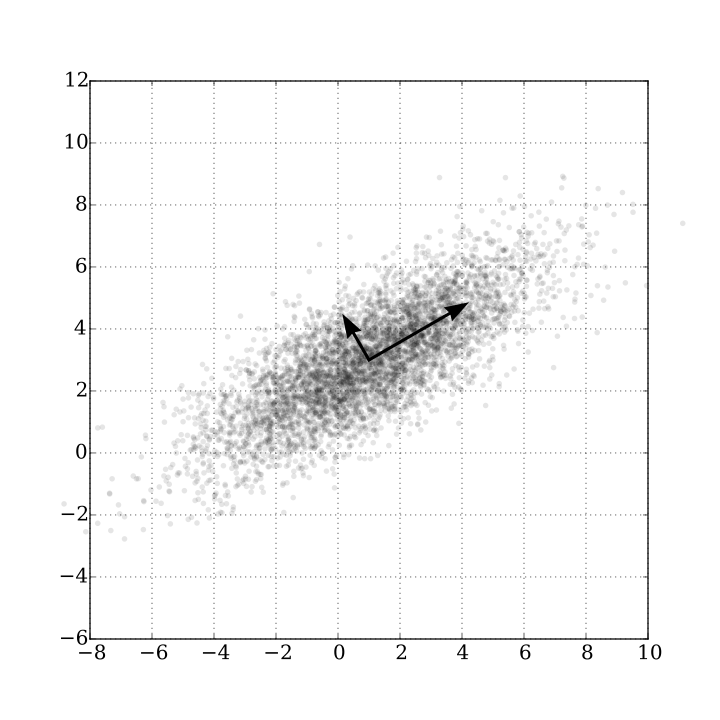
PCA

Prinical Component Analysis

NLS

Non-linear Least Squares: \( E(x) = \factor\sum_{i}^N \left\|f_i\left(x_{i_1}, ... ,x_{i_j}\right)\right\|^2 = \factor\sum_{i=1}^N \res_i^T \res_i = \factor\res^T\res \)

Levenberg-Marquardt step:
\( \Delta x = -(J^TJ + \lambda I)^{-1}J^T\res \)

Related work

point to point
\(\newcommand{\ppDistFull}{\R\pp_i + \pos - \pq_i} E = \sum_{i=1}^N \Norm{\ppDistFull}^2 \)

point to plane
\( E = \sum_{i=1}^N (\R\pp_i + \pos - \pq_i) \cdot \nq_i \)

plane to plane (GICP)
\( \newcommand{\ppDist}{d(\pp_i,\pq_i)} \newcommand{\gicpInfMatrix}{(\R \hat\Cov_{\pp_i}\R^T + \hat\Cov_{\pq_i})^{-1}} E = \sum_{i=1}^N \ppDist^T \gicpInfMatrix \ppDist \)

Bentwing 2015

Approach

composite cubic Bezier curve 0 1 2

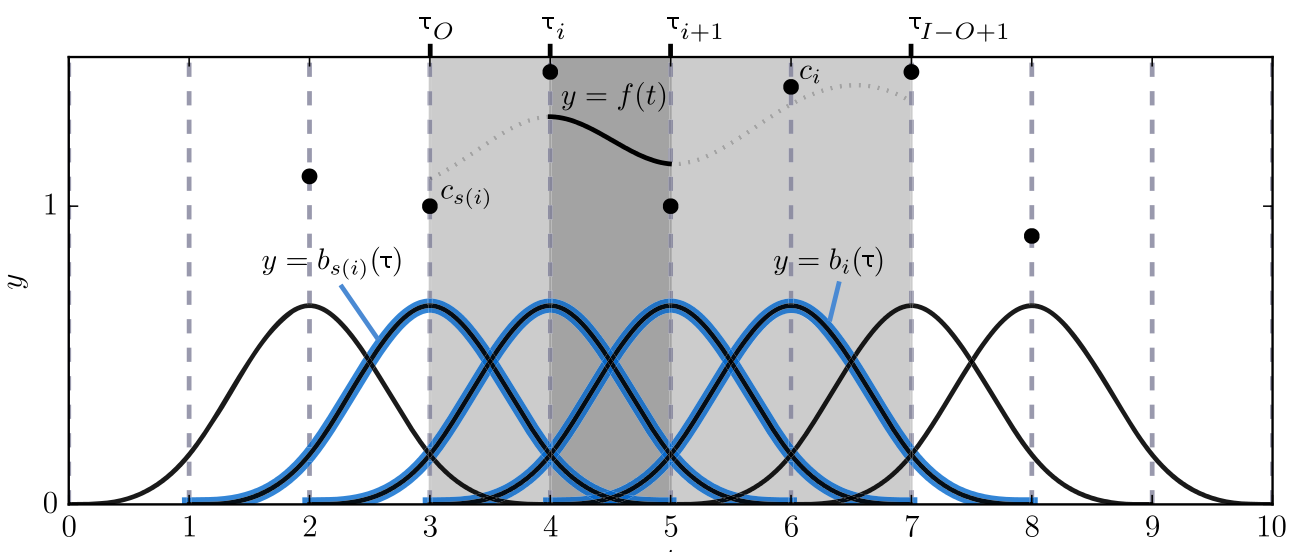
cubic B-spline

cumulative quaternion B-spline \( \quat\curr = \quat_0 \prod_{i=1}^n \exp \big( \tilde{N}_i^k\curr \log(\quat_{i-1}^{-1}\quat_{i}) \big) \\ \newcommand{\NC}{ \frac{1}{6} \begin{bmatrix} 0 & 1 & -2 & 1 \\ 0 & -3 & 3 & 0 \\ 0 & 3 & 3 & 0 \\ 6 & 5 & 1 & 0 \end{bmatrix} } \tilde{N}(u) = [u^3, u^2, u, 1] \NC \\ \)

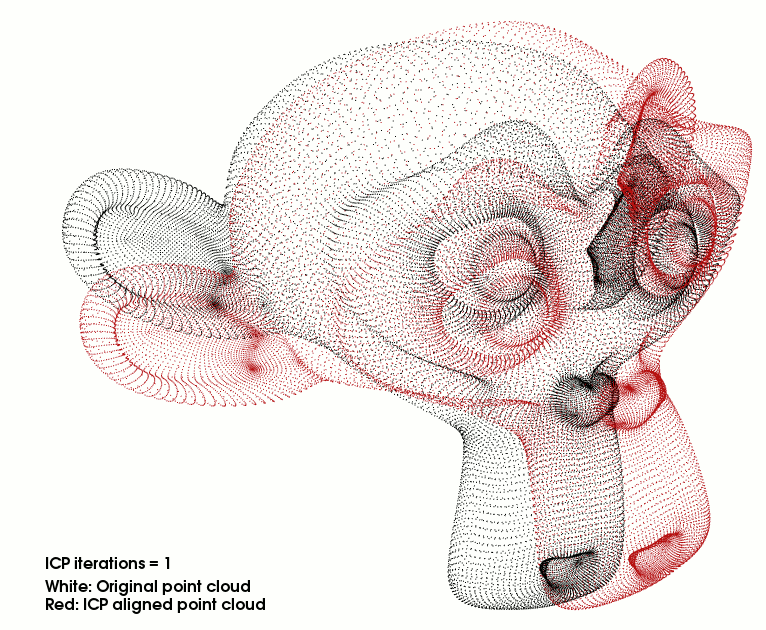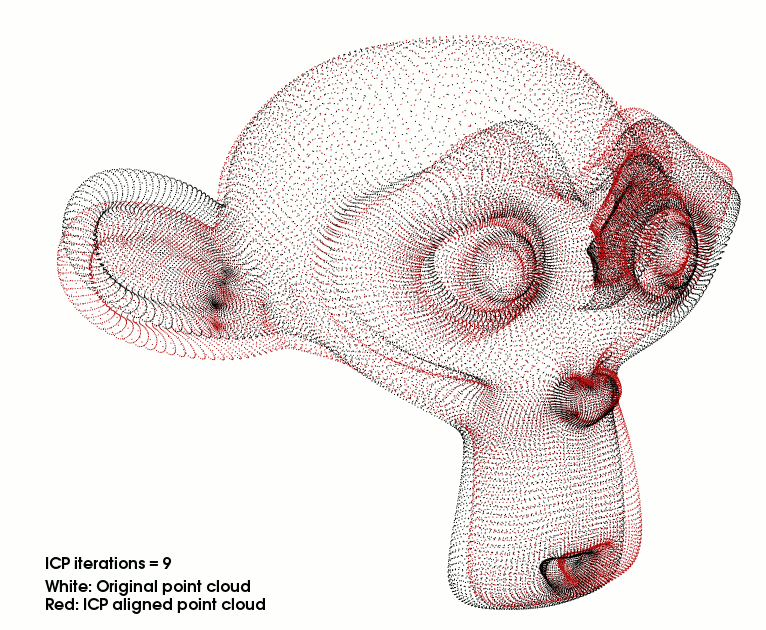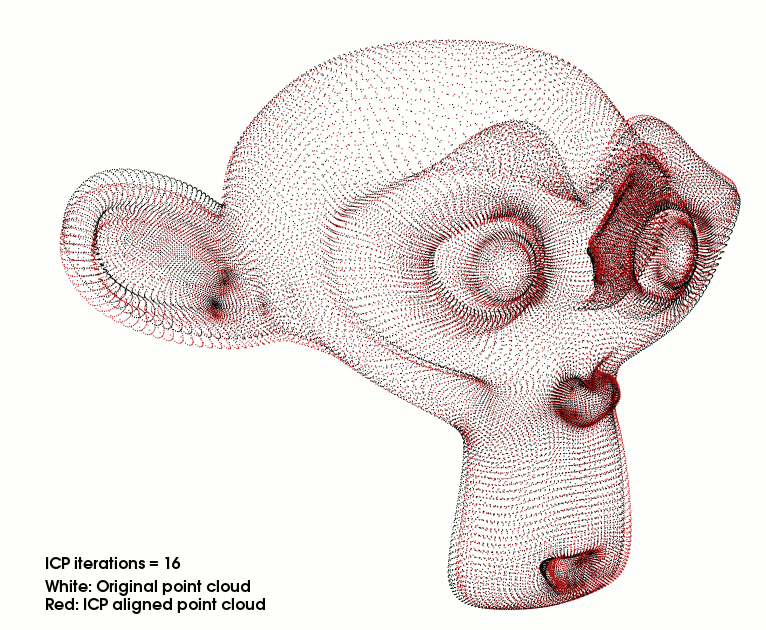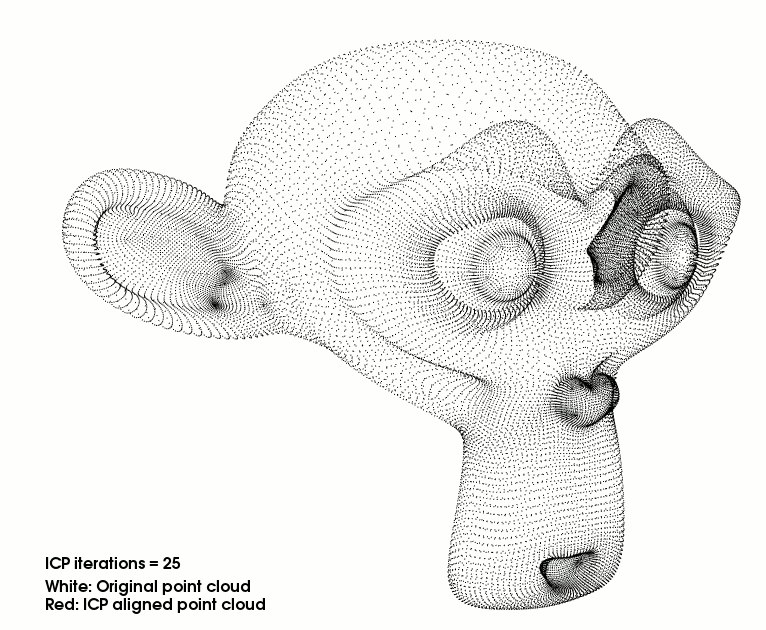
Algorithm

//in:   L Lidar scans    M IMU measurements
//out:  T Trajectory
T = initializeFromIMU(M)
for (i=0 , i < nsweeps , i++ ){
  S[i] = unprojectAndAccumulate(L[i*k],...,L[i*k+k])
  S[i].undistordAndComputeSurfel(T)
  if(i>0){
    imuMatches = imuDeviations(T,M[i-1],...,M[i+1])
    for (j=0 , j < nicp , j++){
      surfelMatches = kdTreeNNLookup(S[i],S[i-1])
      T = NLS(T,surfelMatches,imuMatches)
      S[i].updateSurfelWorldPositions(T)
    }
  }
}

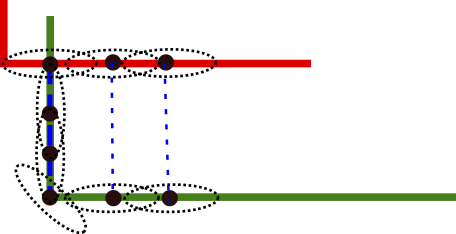
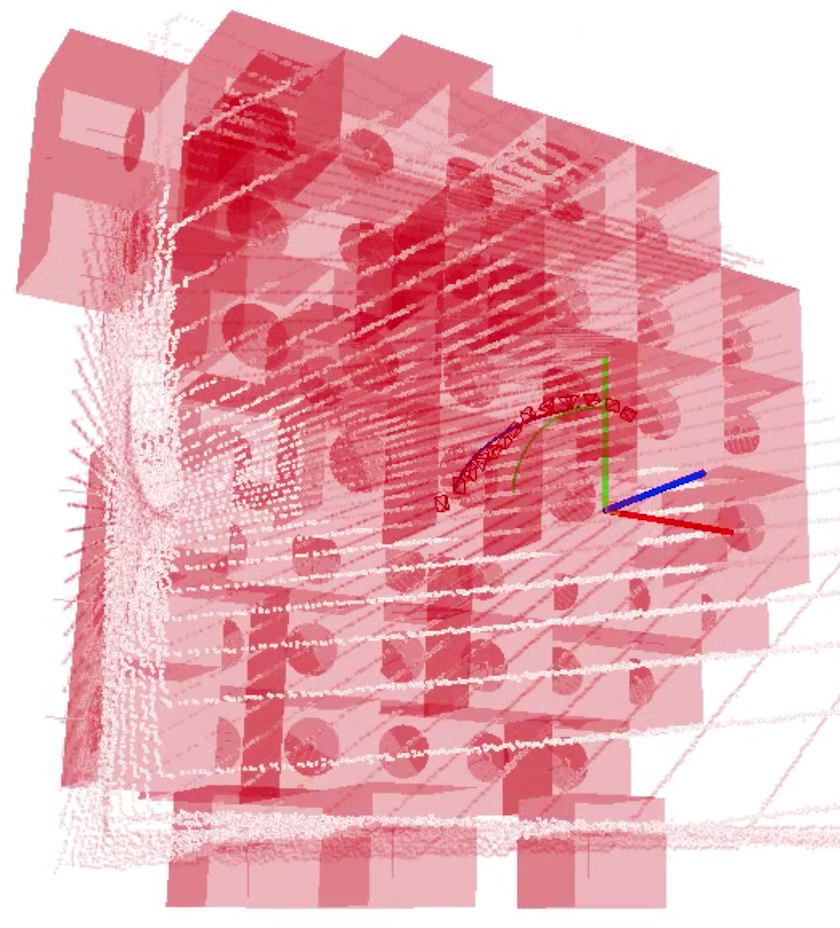
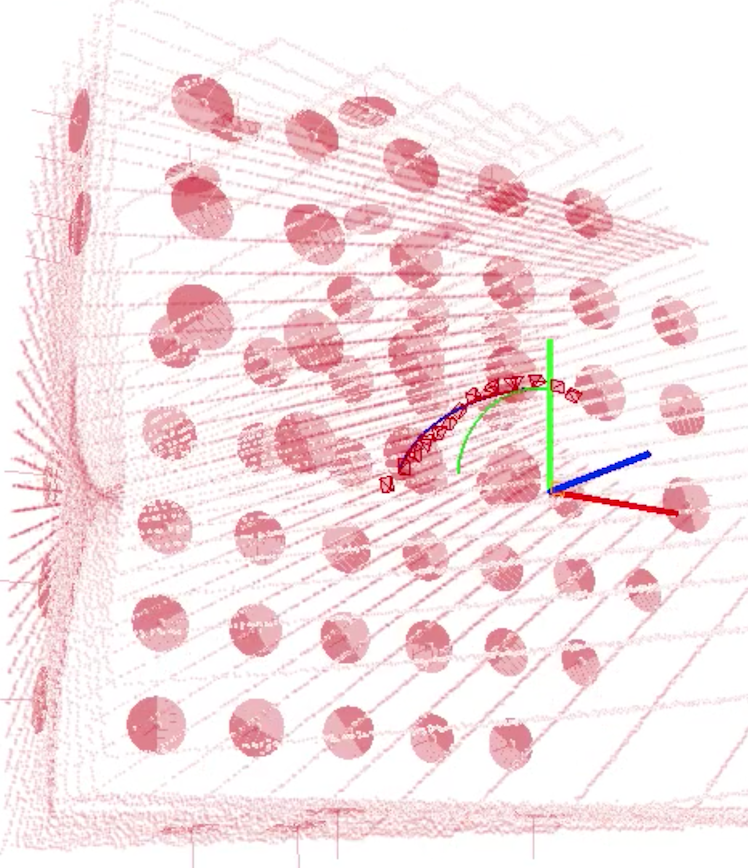
Voxels and Surfels

\( P(\{\point_i\} \text{ describes plane}) = 2\frac{\eigmiddle-\eigsmall}{\eigsum} \)

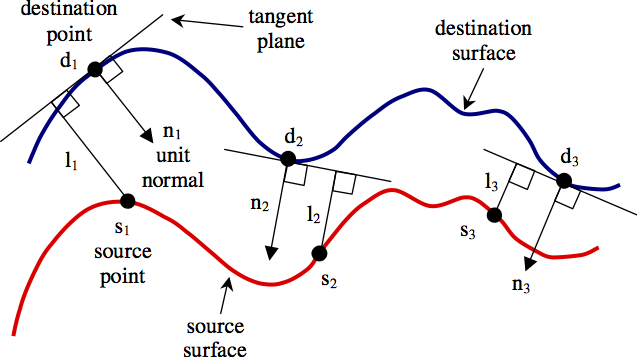
Surfel Matches

Model Optimization
imuMatches:
\( \newcommand{\ppDistAbsSurfel}{\bar{d}(a_i,b_i)} \newcommand{\surfelTuple}{(\mean,\normal,\hat\Cov)} \begin{align} \base \eres_\angVel &= \base\tilde\angVel(\timeVar_k) - \base\angVel(\timeVar_k) - \bias_\angVel(\timeVar_k) \\ \base \eres_\acc &= \base\tilde\acc(\timeVar_k) - \bar\quat(\timeVar_k)\gravity - \base\acc(\timeVar_k) - \bias_\acc(\timeVar_k) \end{align} \)

surfelMatches:
\( \begin{align} \ppDistAbsSurfel &= \R_{a_i}\mean_{a_i} + \pos_{a_i} - (\R_{b_i}\mean_{b_i}+\pos_{b_i} )\nonumber \\ \eres_{a_i,b_i} &= \ppDistAbsSurfel^T (\R_h \hat\Cov_{a_i}\R_h^T + \R_k \hat\Cov_{b_i} \R_k^T)^{-1} \ppDistAbsSurfel \\ \\ \end{align} \) combined: \( E = (1-\alpha)\sum_{i=0}^{N} \eres_{a_i,b_i} + \alpha\sum_{j=1}^M\left( \eres_{\angVel_j}^T\Sigma_\angVel^{-1}\eres_{\angVel_j} + \eres_{\acc_j}^T\Sigma_\acc^{-1}\eres_{\acc_j} \right) \)

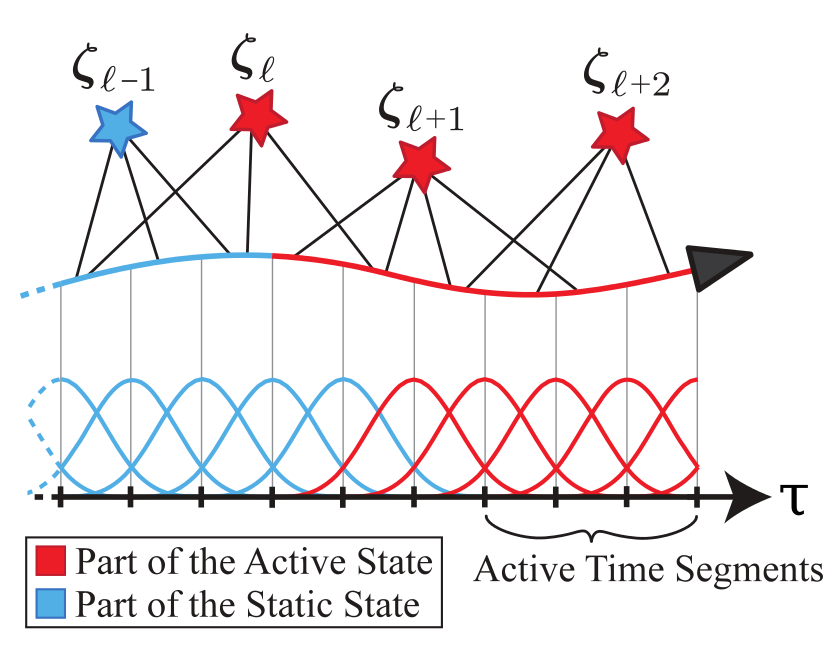
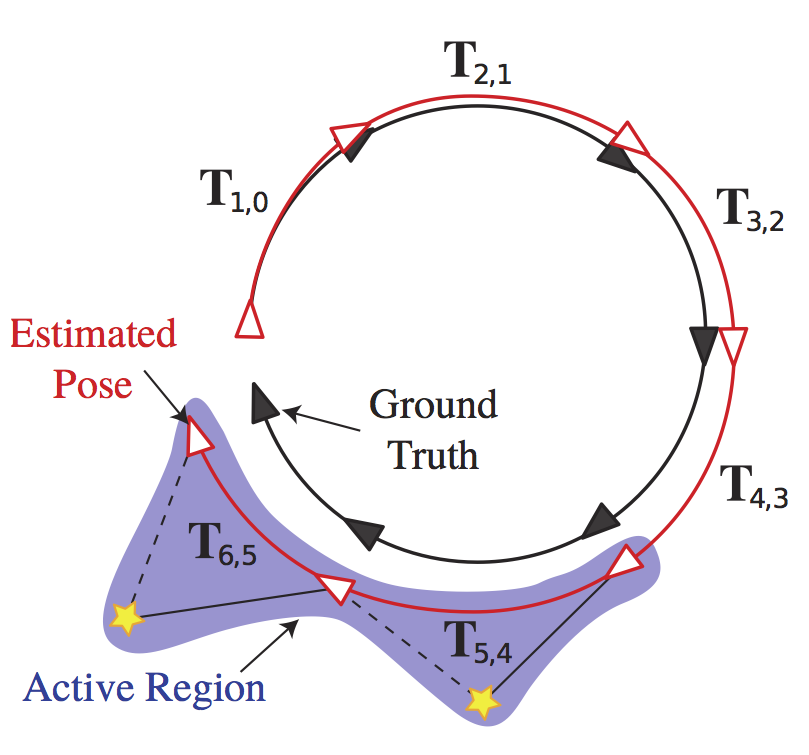
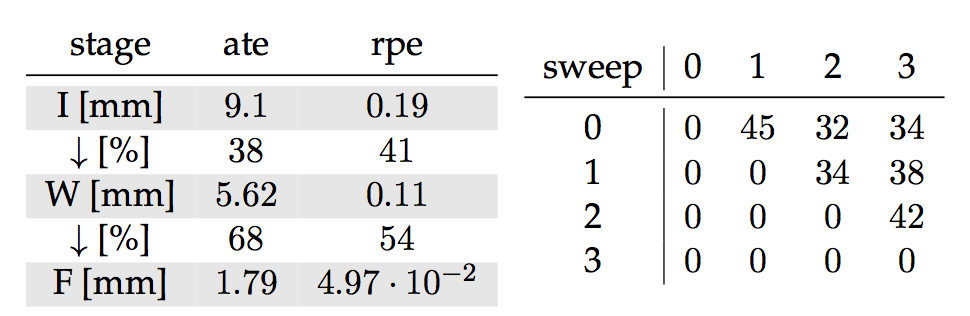
Time-windowed optimization

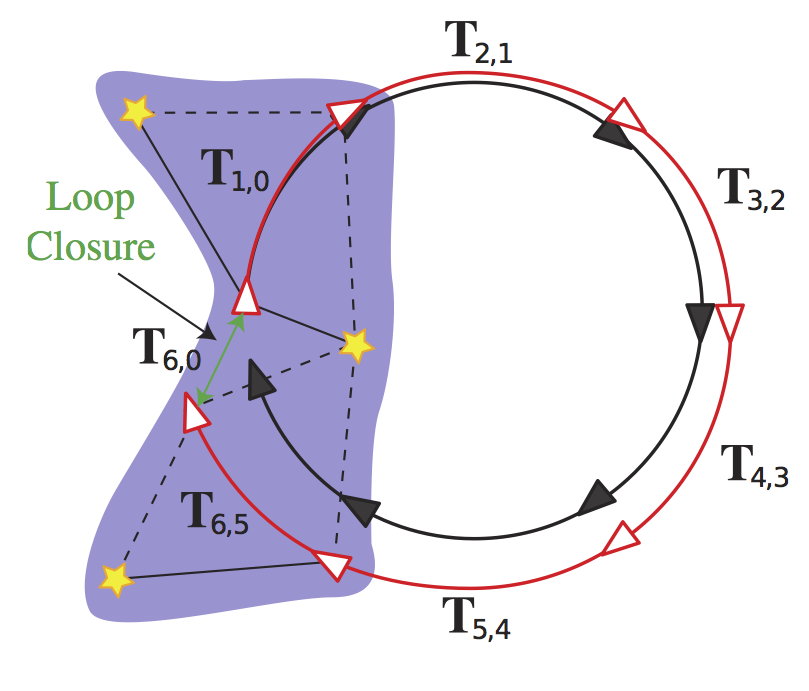
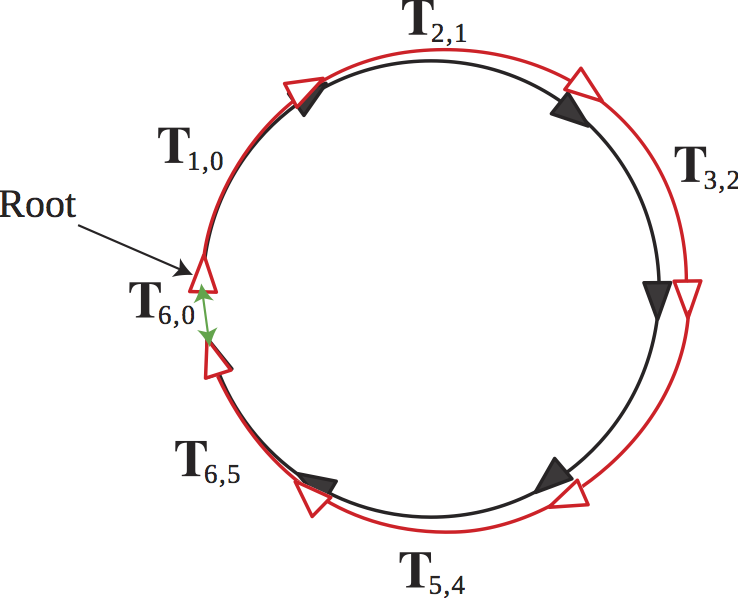
Global optimization

Evaluation

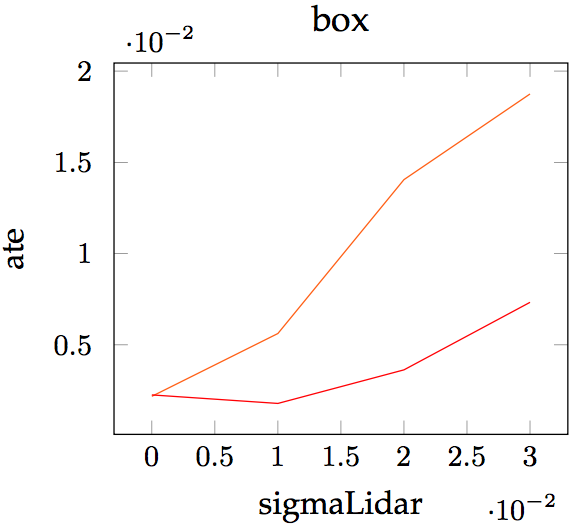
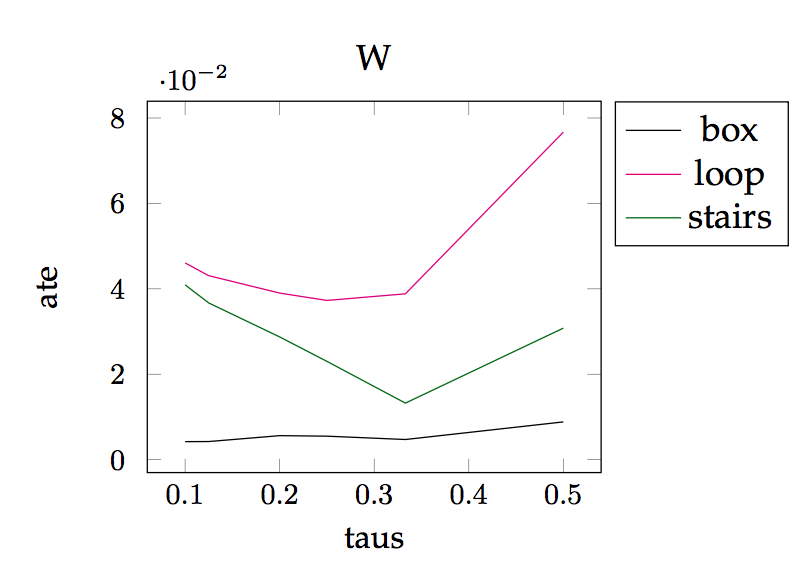
Noise and knot spacing

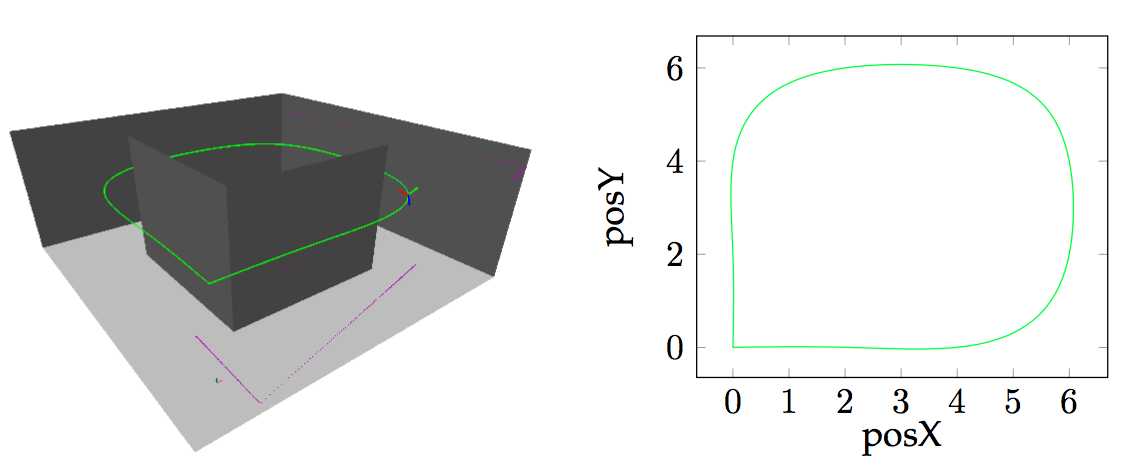
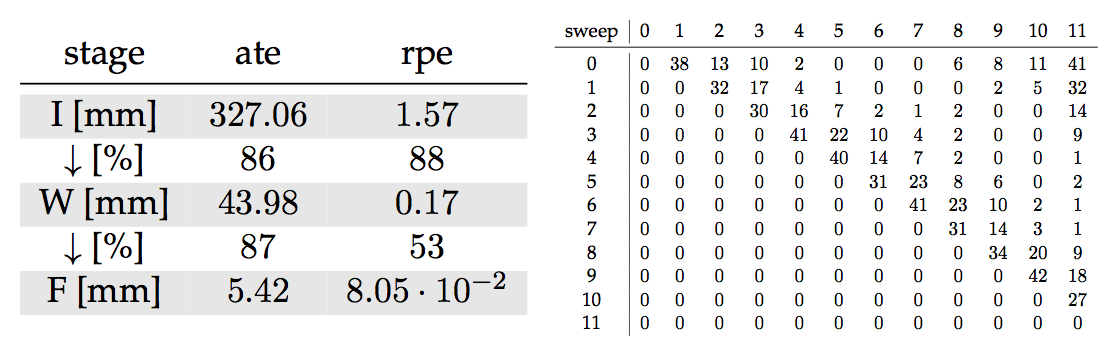
box

loop

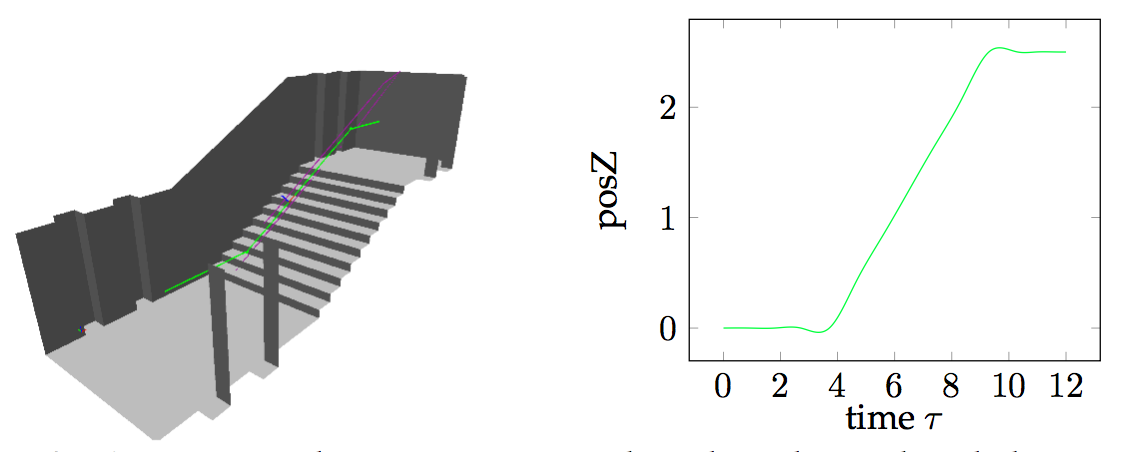
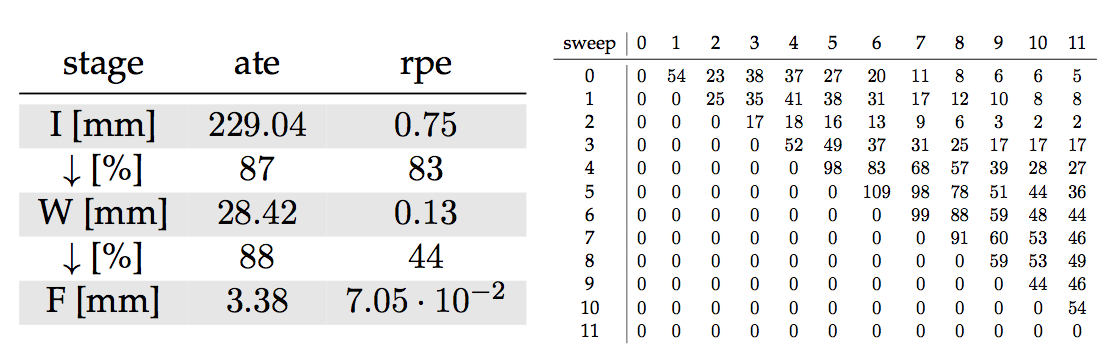
stairs